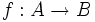 را تابع ثابت می گوییم هر گاه برد آن یک مجموعه تک عضوی باشد. به عبارت دیگر تابع ثابت هر عضو از دامنه خود را تنها به یک مقدار ثابت متناظر می کند.
را تابع ثابت می گوییم هر گاه برد آن یک مجموعه تک عضوی باشد. به عبارت دیگر تابع ثابت هر عضو از دامنه خود را تنها به یک مقدار ثابت متناظر می کند. پس ضابطه تابع ثابت f از مجموعه A در مجموعه B را می توان به این صورت نوشت
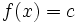 که در آن c مقداری ثابت و همان برد تابع f است.
که در آن c مقداری ثابت و همان برد تابع f است. به عنوان مثال تابع
 یک تابع ثابت است که هر عضو از دامنه خود(مجموعه اعداد حقیقی) را به عدد ثابت 2 متناظر می کند و عدد دو همان برد تابع است.
یک تابع ثابت است که هر عضو از دامنه خود(مجموعه اعداد حقیقی) را به عدد ثابت 2 متناظر می کند و عدد دو همان برد تابع است. نمودار پیکانی زیر نحوه عملکرد تابع ثابت را نشان می دهد:
مشاهده می شود این تابع هر عضو از دامنه(A) خود را به یک مقدار ثابت c متناظر می کند.
به عبارت دقیق تر تابع فوق یک تابع ثابت از مجموعه A به مجموعه تک عضوی {c} است که می توان این مطلب را اینگونه نوشت:
تابع
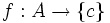 با ضابطه
با ضابطه 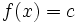
- به دلیل اینکه در حساب دیفرانسیل و انتگرال معمولا با توابع حقیقی و اعداد حقیقی کار می کنیم تابع ثابت معمولا به این صورت تعریف می شود:
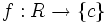 با ضابطه
با ضابطه 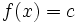 را تابعی ثابت می گوییم. این تابع هر عدد حقیقی را به یک مقدار ثابت چون c متناظر می کند.
را تابعی ثابت می گوییم. این تابع هر عدد حقیقی را به یک مقدار ثابت چون c متناظر می کند. نمودار تابع یک تابع ثابت همواره یک خط موازی محور X ها است. به عنوان مثال نمودار تابع ثابت
 به این صورت است:
به این صورت است:
- بررسی ویژگی های توابع ثابت:
- توابع ثابت توابعی غیر یک به یک می باشند.
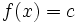 هر عضو از دامنه خود را به C متناظر می کند پس:
هر عضو از دامنه خود را به C متناظر می کند پس: 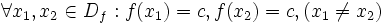 که این نشان می دهد تابع ثابت یک به یک نمی باشد چرا که دو زوج مرتب با مولفه اول متمایز و با مولفه دوم یکسان در آن یافت می شود.
که این نشان می دهد تابع ثابت یک به یک نمی باشد چرا که دو زوج مرتب با مولفه اول متمایز و با مولفه دوم یکسان در آن یافت می شود.
- توابع ثابت معکوس پذیر نمی باشند.
- تابع ثابت
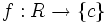 تابعی پوشا است.
تابعی پوشا است.
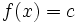 را در نظر بگیرید. برای اثبات پوشا بودن باید نشان داد:
را در نظر بگیرید. برای اثبات پوشا بودن باید نشان داد:
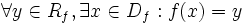
حال در تابع ثابت داریم:
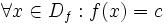
که این نشان می دهد برای هر عضو از برد یعنی C یک عضو از دامنه چون x وجود دارد که x به C متناظر شود یا به عبارتی
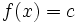 که این دلیل بر پوشا بودن f است.
که این دلیل بر پوشا بودن f است.
- تابع ثابت زوج می باشند به استثنای تابع
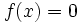 که هم زوج و هم فرد است.
که هم زوج و هم فرد است.
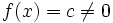 را در نظر بگیرید. دامنه این تابع مجموعه اعداد حقیقی است. لذا شرط اولیه زوج یا فرد بودن تابع یعنی متقارن بودن دامنه را دارا است.
را در نظر بگیرید. دامنه این تابع مجموعه اعداد حقیقی است. لذا شرط اولیه زوج یا فرد بودن تابع یعنی متقارن بودن دامنه را دارا است. 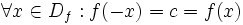 پس تابع مذکور زوج است.
پس تابع مذکور زوج است. حال تابع
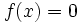 را در نظر بگیرید. داریم:
را در نظر بگیرید. داریم: 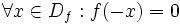
همچنین می توان نوشت:
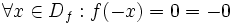
پس تابع مذکور هم در شرط زوج بودن و هم در شرط فرد بودن تابع صدق می کند پس هم زوج و هم فرد است.
نظرات شما عزیزان:

